- Blog
-
Teacher Resources
- Shop
-
Video Library
-
Math Mystery Video Hooks
>
- Case of the 100 Missing Treats
- Case of The Abducted Alien
- Case of The Alien Apocalypse
- Case of The Angry Adder
- Case of The Bee Bandits
- Case of the Christmas Chaos
- Case of the Cursed Classrooms
- Case of The Disappearing Donuts
- Case of The Divided Dragon's Division Review
- Case of The Dream Snatcher
- Case of The Egg Thief
- Case of The Forgetful Pharaoh
- Case of The Furious Falls Winds
- Case of the Giant Goblin
- Case of The Gobbler's Curse
- Case of The Graduation Gremlins
- Case of the Great Zoo Escape
- Case of The Greedy Gnome
- Case of the Halloween Heist
- Case of the Heartbroken Heroes
- Case of the Invisible Illusionist - Integers Math Mystery Activity
- Case of the Jumpy Jack-O-Lanterns Halloween Math Mystery
- Case of The Jungle Joker
- Case of The Kidnapped Groundhog
- Case of The Litterbug
- Case of the Lost Leprechaun
- Case of the Magnificent Growth Mindset
- Case of The Mathattan Meltdown
- Case of Mean Mountain
- Case of The Millennium Bug
- Case of the Mirror Madness
- Case of The Misplaced Pot of Gold
- Case of the Missing Campers
- Case of the Missing Macaw
- Case of The Monster Mix-Up
- Case of the Never-Ending Rain
- Case of the Outback Outlaw
- Case of The Phantom Phoenix
- Case of the Pickpocketing Pirate
- Case of The Poisonous Pizzas
- Case of The Puzzled Pirate
- Case of the Red Envelope Riddles
- Case of The Robot Robbery
- Case of The Rogue Runner
- Case Of The Rotten Eggs
- Case of The School Invaders
- Case of The Selfish Elf
- Case of The Shogun's Sword
- Case of The Snowman Army
- Case of The Sticky Bank Burglary
- Case of The Super Bad Superhero
- Case of the Thanksgiving Thief
- Case of The Thankless Turkey
- Case of The Time Traveling Troll
- Case of The Tricking Treat
- Case of the Troublesome Trickster
- Case of The Valentine Villain
- Case of the Vanishing Valentines
- Case of The Vengeful Vampire
- Case of The Wacky Wild West
- Case of The Zombie Elves
- Junior Reading Mysteries >
-
Private Eye CSI Literacy Mystery Video Hooks
>
- The Case of the Actor's Accident
- The Case of the Critter Chaos
- The Case of the Devious Duo
- The Case of the Easter Egg Scapade
- The Case of the Grumpy Ghost
- The Case of the Masked Menace
- The Case of the Pilfered Pencils
- The Case of the Reckless Reindeer
- The Case of the Ruined Research
- The Case of the Stolen Surfboard
- The Case of the Turkey Tournament
- The Case of the Wacky Wand
-
Reading Mystery Video Hooks
>
- Burrow Slime
- EGGpocalypse
- Fool's Gold Read Mystery
- Forest Grime - Reading Mystery
- Haunting Hat - Reading Mystery
- Humpty's Fall Reading Mystery
- Knight's Tail
- Poisoned Valentine
- Rescue Rudolph
- Stolen Time
- Teacher Toads - Reading Mystery
- Turkey Trouble!
- Twinkle's Lost Shine
- Which Witch? - Reading Mystery
- Wizard Blizzard
- Math Quest Video Hooks >
-
A-Z Letter Detectives Video Hook
>
- The Case of the Alien's Apples
- The Case of the Banana Bandit
- The Case of the Cat's Cookies
- The Case of the Dragon's Diamonds
- The Case of the Eagle's Eggs
- The Case of the Frog's Flowers
- The Case of the Ghost's Gumballs
- The Case of the Hippo's Hat
- The Case of the Iguana's Ice Cream
- The Case of the Jaguar's Jellybeans
- The Case of the Kangaroo's Kite
- The Case of the Lion's Lollipops
- The Case of the Monster's Map
- The Case of the Ninja's Necklace
- The Case of the Octopus's Oar
- The Case of the Pirate's Pizza
- The Case of the Queen's Quiver
- The Case of the Robot's Rocket
- The Case of the Sloth's Skateboard
- The Case of the Turtle's Toys
- The Case of the Unicorn's Umbrella
- The Case of the Vampire's Violin
- The Case of the Wizard's Wand
- The Case of the X-Hero's X-Ray
- The Case of the Yeti's Yo-Yo
- The Case of the Zebra's Zucchinnis
-
Math Minute Missions
>
- Math Minute Mission Challenge #1
- Math Minute Mission Challenge #2
- Math Minute Mission #3
- Math Minute Mission #4
- Math Minute Mission #5
- Math Minute Mission #6
- Math Minute Mission Challenge #7
- Math Minute Mission #8
- Math Minute Mission #9
- Math Minute Mission #10
- Math Minute Mission #11
- Math Minute Mission #12
- Math Minute Mission #13
- Math Minute Mission #14
- Math Minute Mission #15
- Math Minute Mission #16
- Math Minute Mission #17
- Background Music >
-
Math Mystery Video Hooks
>
- TPT
- About
- Privacy Policy
- New Page
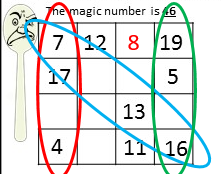
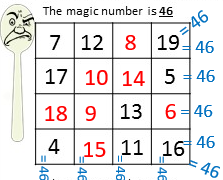
Below I will go through each level and show an example of how I would tackle each, including my thought process. I believe if you can get the idea of a way to look at these, then working through each should be much less frustrating! Then Dodger's horrible party can be put to an end!
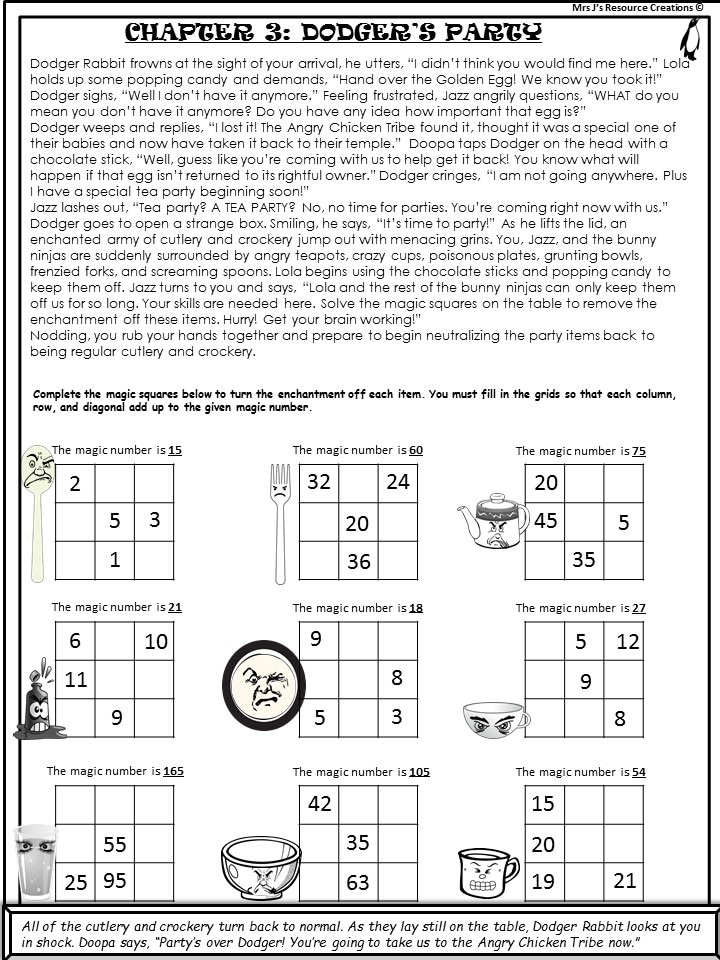
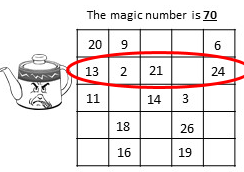
EASY LEVEL
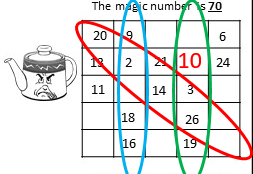
The same strategy applies for the harder ones. I'll demonstrate these steps in both the 4 x 4 grids in MEDIUM, and the 5 x 5 Grids in HARD.
MEDIUM LEVEL
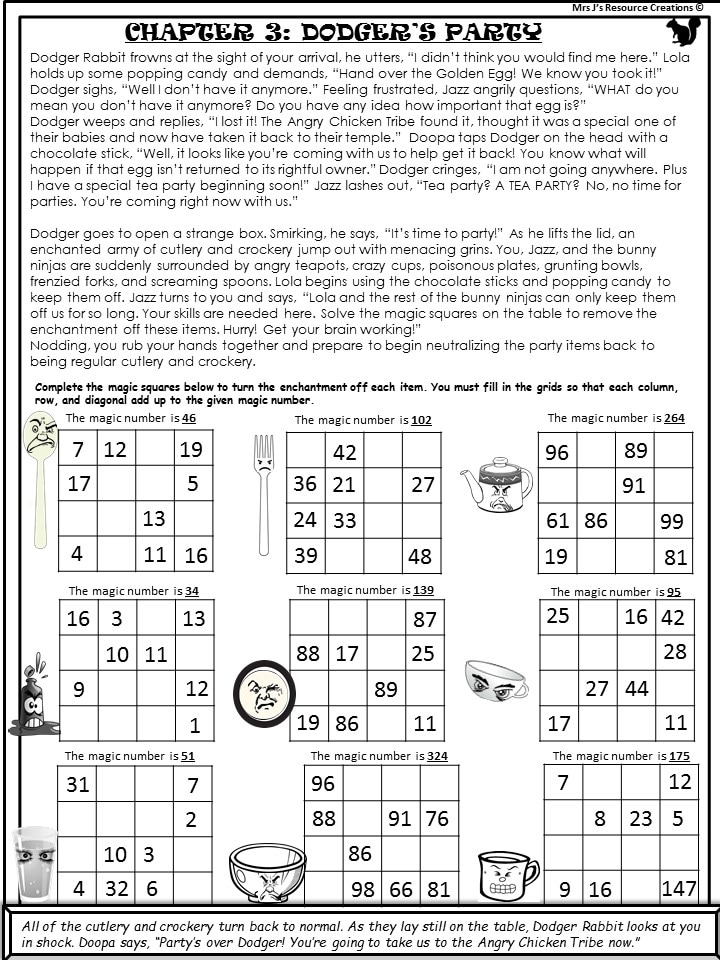
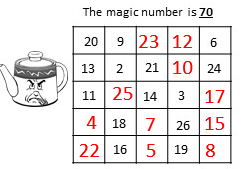
For the HARD Level of Dodger's Party, the Magic Squares are 5 x 5. These look a little bit more daunting than they really are . . . but, they do require a bit more skill in hunting for that secret row, column or diagonal to help progress through the square smoothly. More math is involved too since more numbers will be required to be summed up, and the magic numbers get bigger.
Again, I will demonstrate with the same steps used above (Easy and Medium) to show the completion of the more challenging one. HARD LEVEL
Achieve Chapter 3 of the Math Quest using the same strategy as in the above demonstrations. You just may need to crank up the brain power a bit more to tackle these though. Watch out cranky teapot!
So that's the special strategy to conquering the challenge faced at Dodger's Party.
The full resource that I have been referring to during this Magic Square post is down below. You can click through to find out more about it in my TPT store. It is a fun math quest involving six challenging chapters to work through. Students can end up with one of four possible endings. A fun video hook is also provided to introduce the activity to your students and create excitement. Great for extra practice and review, early finishers, enrichment, or the sub tub. Individual levels can be purchased separately, or bundled at a reduced price to allow for differentiation.
1 Comment
Amy Donison
7/11/2017 07:34:40 pm
You are brilliant!
Reply
Leave a Reply. |
Categories
All
AuthorA 21st century School Teacher, Mother, and Wife. This website uses marketing and tracking technologies. Opting out of this will opt you out of all cookies, except for those needed to run the website. Note that some products may not work as well without tracking cookies. Opt Out of Cookies |
|
TPT Store: Mrs J's Resource Creations
|
- Blog
-
Teacher Resources
- Shop
-
Video Library
-
Math Mystery Video Hooks
>
- Case of the 100 Missing Treats
- Case of The Abducted Alien
- Case of The Alien Apocalypse
- Case of The Angry Adder
- Case of The Bee Bandits
- Case of the Christmas Chaos
- Case of the Cursed Classrooms
- Case of The Disappearing Donuts
- Case of The Divided Dragon's Division Review
- Case of The Dream Snatcher
- Case of The Egg Thief
- Case of The Forgetful Pharaoh
- Case of The Furious Falls Winds
- Case of the Giant Goblin
- Case of The Gobbler's Curse
- Case of The Graduation Gremlins
- Case of the Great Zoo Escape
- Case of The Greedy Gnome
- Case of the Halloween Heist
- Case of the Heartbroken Heroes
- Case of the Invisible Illusionist - Integers Math Mystery Activity
- Case of the Jumpy Jack-O-Lanterns Halloween Math Mystery
- Case of The Jungle Joker
- Case of The Kidnapped Groundhog
- Case of The Litterbug
- Case of the Lost Leprechaun
- Case of the Magnificent Growth Mindset
- Case of The Mathattan Meltdown
- Case of Mean Mountain
- Case of The Millennium Bug
- Case of the Mirror Madness
- Case of The Misplaced Pot of Gold
- Case of the Missing Campers
- Case of the Missing Macaw
- Case of The Monster Mix-Up
- Case of the Never-Ending Rain
- Case of the Outback Outlaw
- Case of The Phantom Phoenix
- Case of the Pickpocketing Pirate
- Case of The Poisonous Pizzas
- Case of The Puzzled Pirate
- Case of the Red Envelope Riddles
- Case of The Robot Robbery
- Case of The Rogue Runner
- Case Of The Rotten Eggs
- Case of The School Invaders
- Case of The Selfish Elf
- Case of The Shogun's Sword
- Case of The Snowman Army
- Case of The Sticky Bank Burglary
- Case of The Super Bad Superhero
- Case of the Thanksgiving Thief
- Case of The Thankless Turkey
- Case of The Time Traveling Troll
- Case of The Tricking Treat
- Case of the Troublesome Trickster
- Case of The Valentine Villain
- Case of the Vanishing Valentines
- Case of The Vengeful Vampire
- Case of The Wacky Wild West
- Case of The Zombie Elves
- Junior Reading Mysteries >
-
Private Eye CSI Literacy Mystery Video Hooks
>
- The Case of the Actor's Accident
- The Case of the Critter Chaos
- The Case of the Devious Duo
- The Case of the Easter Egg Scapade
- The Case of the Grumpy Ghost
- The Case of the Masked Menace
- The Case of the Pilfered Pencils
- The Case of the Reckless Reindeer
- The Case of the Ruined Research
- The Case of the Stolen Surfboard
- The Case of the Turkey Tournament
- The Case of the Wacky Wand
-
Reading Mystery Video Hooks
>
- Burrow Slime
- EGGpocalypse
- Fool's Gold Read Mystery
- Forest Grime - Reading Mystery
- Haunting Hat - Reading Mystery
- Humpty's Fall Reading Mystery
- Knight's Tail
- Poisoned Valentine
- Rescue Rudolph
- Stolen Time
- Teacher Toads - Reading Mystery
- Turkey Trouble!
- Twinkle's Lost Shine
- Which Witch? - Reading Mystery
- Wizard Blizzard
- Math Quest Video Hooks >
-
A-Z Letter Detectives Video Hook
>
- The Case of the Alien's Apples
- The Case of the Banana Bandit
- The Case of the Cat's Cookies
- The Case of the Dragon's Diamonds
- The Case of the Eagle's Eggs
- The Case of the Frog's Flowers
- The Case of the Ghost's Gumballs
- The Case of the Hippo's Hat
- The Case of the Iguana's Ice Cream
- The Case of the Jaguar's Jellybeans
- The Case of the Kangaroo's Kite
- The Case of the Lion's Lollipops
- The Case of the Monster's Map
- The Case of the Ninja's Necklace
- The Case of the Octopus's Oar
- The Case of the Pirate's Pizza
- The Case of the Queen's Quiver
- The Case of the Robot's Rocket
- The Case of the Sloth's Skateboard
- The Case of the Turtle's Toys
- The Case of the Unicorn's Umbrella
- The Case of the Vampire's Violin
- The Case of the Wizard's Wand
- The Case of the X-Hero's X-Ray
- The Case of the Yeti's Yo-Yo
- The Case of the Zebra's Zucchinnis
-
Math Minute Missions
>
- Math Minute Mission Challenge #1
- Math Minute Mission Challenge #2
- Math Minute Mission #3
- Math Minute Mission #4
- Math Minute Mission #5
- Math Minute Mission #6
- Math Minute Mission Challenge #7
- Math Minute Mission #8
- Math Minute Mission #9
- Math Minute Mission #10
- Math Minute Mission #11
- Math Minute Mission #12
- Math Minute Mission #13
- Math Minute Mission #14
- Math Minute Mission #15
- Math Minute Mission #16
- Math Minute Mission #17
- Background Music >
-
Math Mystery Video Hooks
>
- TPT
- About
- Privacy Policy
- New Page